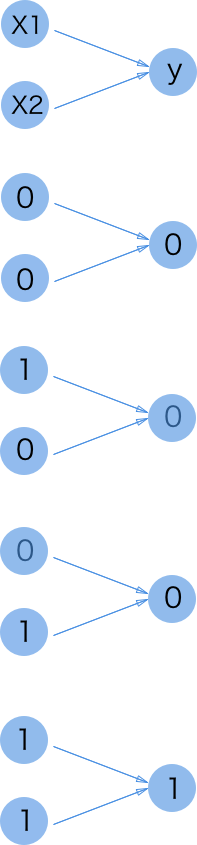
パーセプトロンを理解するために、ANDゲートの結果を教師データとして、重みとバイアスの調節をやってみる。
まず、ANDゲートの概念図なり〜
(0,0)を入力したばあいは、0が出力される。
(1,0)を入力したばあいは、0が出力される。
(0,1)を入力したばあいは、0が出力される。
(1,1)を入力したばあいは、1が出力される。
このような出力結果になるように、pythonにて関数を書いてみる。
スカラーのばあい。
(スカラーという言葉つかいに自信なし。後述のベクトルに合わせて、ためしに、この言葉をつかっている)。
ANDゲートの出力結果になるように、重み(w1,w2)とバイアス(b)には任意の数値を入れてある。
def AND(x1,x2):
w1,w2,b=0.5,0.5,-0.7
y=x1*w1+x2*w2+b
if y<=0:
return 0
else:
return 1
ベクトルをつかったばあい。
def AND(x1,x2):
x=np.array([x1,x2])
w=np.array([0.5,0.5])
b=-0.7
y=np.sum(x*w)+b
if y <=0:
return 0
else:
return 1
ためしてみる。
AND(0,0)
0
AND(1,0)
0
AND(0,1)
0
AND(1,1)
1
OK〜
では、このばあい(任意にとったw1,w2,bの数値、順に0.5、0.5,-0.7のばあい)1と0に分かれるx1,x2の領域は、どのようになっているか。
いままで、ANDゲートを実装することを主眼に置いていたけれど、以下、入力値(0,0)、(1,0),(0,1),(1,1)にこだわらず、あくまでも、どのような数値を入力すれば、1と0になるのか、みてみよう。
もういちど、作成した関数をみてみる〜
def AND(x1,x2):
w1,w2,b=0.5,0.5,-0.7
y=x1*w1+x2*w2+b
if y<=0:
return 0
else:
return 1
y=x1*w+x2*w2+bに、
w1=0.5、w2=0.5,b=-0.7を代入する。
y=0.5×1+0.5×2-0.7
このさい、0が閾値になるので、y=0を代入。
0=0.5×1+0.5×2-0.7
0.7=0.5×1+0.5×2
0.5×2=-0.5×1+0.7
両辺を0.5で割る
x2=x1+0.7/0.5
x2=x1+1.4
たぶん大丈夫。
x2=x1+1.4のグラフを書いてみよ〜。
import matplotlib.pyplot as plt
import numpy as np
x1=np.arange(-1,1.1,0.1)
x2=x1+1.4
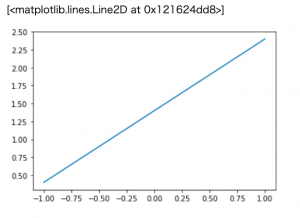
色を、つけてみよう。
plt.fill_between(x1,x2)
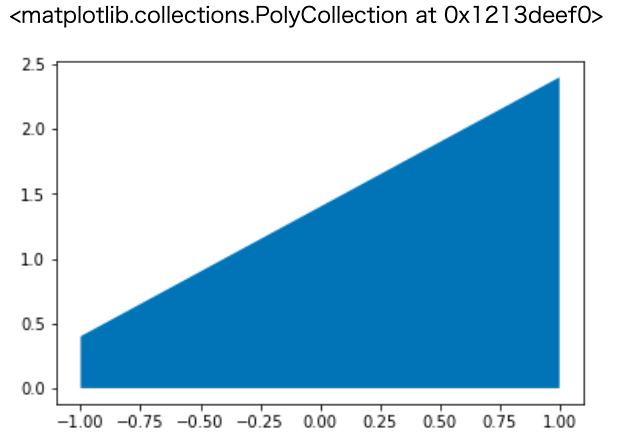
たぶん…ブルーの領域のx1,x2を入力すれば、出力はゼロだったりしそう…
ためしてみよう。
たとえば、
(x1,x2)=> ?
(0.25,0.25)=> 0
(0.5,1.5)=>1
(0,1.5)=>1
(0,1,4)=>0
よさそう。
ちなみに、x10のさかいは、1.4..だねぇ。
参考:「ゼロから作るDeep Learning」(斎藤康毅/オライリー・ジャパン)