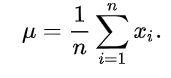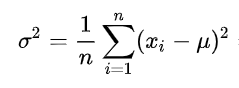定数は1、のように定まった数値。
変わる数値は変数という。
たとえば、サイコロを振ってみよう。
その際の変数をXとする。
Xは、ときには1になり、ときには2になり….6となる。
そして確率っぽく利用するときは、確率変数と呼ばれ、X=1,2,3,4,5,6となる。
オッケー、ここからpythonで、カンタンなプログラムを書いてみよう〜
まずライブラリーを読み込む。
from numpy.random import randint
from scipy import stats
import matplotlib.pyplot as plt
確率変数をリスト化する。
dice_random_variable = [1,2,3,4,5,6]
1〜6までの確率(1/6)の合計(1/6+1/6+1/6+1/6+1/6+1/6=1)
prob_sum = 1
それぞれの目が出る確率。
prob = prob_sum/len(dice_random_variable)
prob
0.16666666666666666
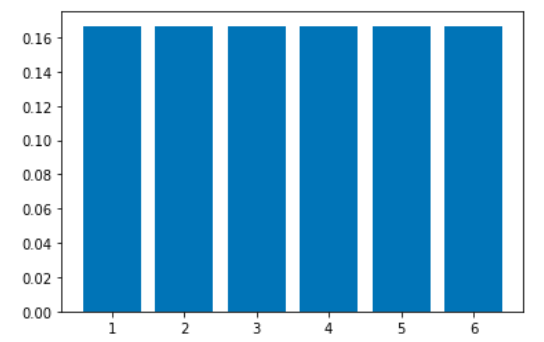
棒グラフで表現してみる。
plt.bar(dice_random_variable,prob)
mean=sum(dice_random_variable )*prob
mean
3.5
var=((mean-1)**2+(mean-2)**2+(mean-3)**2+(mean-4)**2+(mean-5)**2+(mean-6)**2)*prob
var
2.9166666666666665
参考:
実践python データサイエンス
11-2 離散型確率分布と確率質量変数 / 統計WEB
標準偏差/ウィキペディア