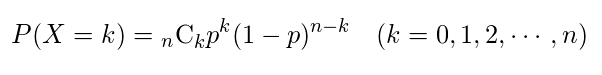二項分布

10円玉を投げたとき､表が出たり､裏が出たりする｡

その際の確率変数を､表を１､裏を０とする｡

P(X=1) = P
p(X=0) =1-P

n回投げたとき､表が出る確率を描く分布を二項分布というらしい｡

関数は以下の通り｡うーん､むつかしい｡

具体的にやってみよう｡

３回投げたとき､３回とも表が出る場合､

(10×9×8 / 3×2×1) ×（0.5×0.5×0.5×0.5）×(0.5×0.5×0.5×0.5×0.5×0.5×0.5) 
=120 × 0.125 × 0.0078125
=0.1171875

計算がたいへん､

というわけで､pythonのライブラリーをつかって､やってみる｡

ライブラリーscipyをつかう｡
from scipy.special import comb

comb=comb(10,3)
Pa=(1/2)**3
Pb=(1/2)**7
ans = comb*Pa*Pb
0.1171875

ライブラリーをつかえばカンタンにできてしまうが､そのクラスやアトリビュートは､ぜったい覚えられないだろうよ｡

じゃ､コイン10回投げたとき､表が出る回数の確率を求めてみよー｡

from scipy.stats import binom

n = 10
p = 1/2
x=range(n+1)
y = binom.pmf(x,n,p)
y

array([0.00097656, 0.00976563, 0.04394531, 0.1171875 , 0.20507813,
       0.24609375, 0.20507813, 0.1171875 , 0.04394531, 0.00976563,
       0.00097656])

 プロットする｡
import matplotlib.pyplot as plt
plt.plot(x,y,’o’)

１０回中､５回投げた場合､いちばん表が出る確率が高いことが分かる｡このへんは直感どおりだねぇ｡0.25%というのが､ちょっと…0.5%の方が俺的にはピンと来たりするけれど…

参考:
実践python データサイエンス/udemy
13-1二項分布 統計WEB